Part 2: VC Dimension - Theorems and Lemmas
By Mohammad Sadil Khan in Computational Theory Deep Learning VC Dimension MLP
September 29, 2022
This is the second part of the VC Dimension and Neural Networks series. This part lists important theorems with proofs and explanations. To know the basics of VC dimension, check Part 1 - VC Dimension - Definition and Examples.
1. Definitions
$\textbf{Dichotomy}:$ A dichotomy of $S=\{x_1,x_2,\cdots,x_m\}$ induced by $h \in \mathscr{H}$ is a partition of S into two disjoint sets $S_1$ and $S_2$ such that $$h(x_i)=\begin{cases} 1 \, \text{if} \, x_i \in S_1 \\ -1 \, \text{if} \, x_i \in S_2\\ \end{cases}$$
Let $\mathscr{H}(S)$ be the set of all labelings or dichotomies that can be realized by $\mathscr{H}$. $$\mathscr{H}(S)=\{ \{ h(x_1),h(x_2),\cdots h(x_m) \}; h \in \mathscr{H} \}$$ If $|\mathscr{H}(S)|=2^{|S|}$, then $S$ is shattered by $\mathscr{H}$.
Since $S$ is chosen randomly, we define $\textbf{Growth Function}$ [1] $$\mathscr{H}[m]=max\{|\mathscr{H}(S)|; |S|=m ; S \subset R^m \}$$
2. Theorem 1 - Radon’s Theorem
$\textbf{Theorem 1 (Radon's Theorem):}$ For every set $S \subset {R}^{d}$ with $|S|=d+2$, $S$ can be divided into two disjoint sets whose convex hulls intersect.
$\textbf{Proof:}$ Let $S=\{x_1,x_2,\cdots,x_{d+2}\} \subset R^{d}$. Then $S$ is a linearly dependent set. Let $S_{aug}=\{[x_1;1],[x_2,;1]\cdots,[x_{d+2};1]\} \subset R^{d+1}$ be the augmented set and it's also a dependent set. Then the equation $$\sum_{i=1}^{d+2}a_i[x_i;1]=0$$ has non-zero solution (not all $a_i=0$) and $\sum_{i=1}^{d+2}a_i=0$.
Let I be the convex hull of $\{x_i:a_i>0\}$ and J be the convex hull of $\{x_i:a_i\leq 0\}$.
$\{x_i:a_i>0\} \cap \{x_i:a_i\leq 0\} =\phi$.
Let $A=\sum_{i:x_i\in I}a_i=-\sum_{j:x_j\in J}a_j$.
Then $\frac{1}{A}\sum_{i=1}^{d+2}a_ix_i=0 \implies \sum_{i:x_i\in I}\frac{a_j}{A}x_j=-\sum_{j:x_j\in J}\frac{a_j}{A}x_j$
So $p=\sum_{i:x_i\in I}\frac{a_j}{A}x_j=-\sum_{j:x_j\in J}\frac{a_j}{A}x_j$
So $p \in I \text{ and } p \in J$.
So, S can be divided into two disjoint sets whose convex hulls intersect.
3. Theorem 2 - $VC(\mathscr{H}) \leq log_2(|\mathscr{H}|)$
$\textbf{Theorem 2:}$ Let $\mathscr{H}$ be a set of binary-valued functions and $\mathscr{H}$ is finite. Then $VC(\mathscr{H}) \leq log_2(|\mathscr{H}|)$.
$\textbf{Proof:}$ Let $VC(\mathscr{H})=d$, then there exists a set of $d$ points such that for every $2^d$ possible labelings, $\exists \, h \in \mathscr{H}$ which can classify the points. Then the cardinality of $\mathscr{H}$ must be greater than $2^d$.
So $|\mathscr{H}|\geq 2^d \implies d \leq log_2(\mathscr{H}) \implies VC(\mathscr{H}) \leq log_2(\mathscr{H})$.;
4. Theorem 3 - Sauer’s Lemma
$\textbf{Theorem 2:}$ Let $VC(\mathscr{H})=d$ and $S$ be a set of $m$ points. Then $$\mathscr{H}[m] \leq \Phi_{d}(m)=\sum\limits_{i=0}^{d} {m\choose i}$$
$\textbf{Proof:}$ We will prove it by induction.
Base Case: For the base case, we have to prove for (1) $d=0$ and arbitrary $m$ and (2) $m=0$ and arbitrary $d$. When $VC(\mathscr{H})=d=0$, it means that no set of points can be shattered, so points can only be labeled one way. So, $\mathscr{H}[m] = 1 \leq \Phi_{d}(m)$. When $m=0$ and $d$ is arbitrary, we can label $0$ points at most $1$ way.
Inductive Step: Let us assume that $\forall m^{'} < m,d^{'} < d$, this statement is true. Let $S=\{x_1,x_2,\cdots,x_m\}$ and $VC(\mathscr{H})=d$. Let $F$ be the set of functions defined only over $S$ such that $\mathscr{H}(S)=F(S)=F$. Then for any set $S^{'} \subset S$ that is shattered by $F$ can be shattered by $\mathscr{H}$. So $VC(F)\leq VC(\mathscr{H})=d$.We now create two disjoint subsets of $F$. For every possible labelings of $\{x_1,x_2,\cdots,x_{m-1}\}$ in F $$F_1=\{ \{f(x_1),f(x_2),\cdots, f(x_{m-1}), 1 \}; f \in F \}$$ $$F_2=F\setminus F_1=\{ \{f(x_1),f(x_2),\cdots, f(x_{m-1}), 0 \}; f \in F \}$$
Then $\forall f_2 \in F_2$, $\exists \, f_1 \in F_1$, such that $f_1(x_i)=f_2(x_i)$, $\forall i=1,2,\cdots, m-1$ and $f_1(x_m)=1, f_2(x_m)=0$.
$$|\mathscr{H}(S)|=|F(S)|=|F_1(S)|+|F_2(S)|$$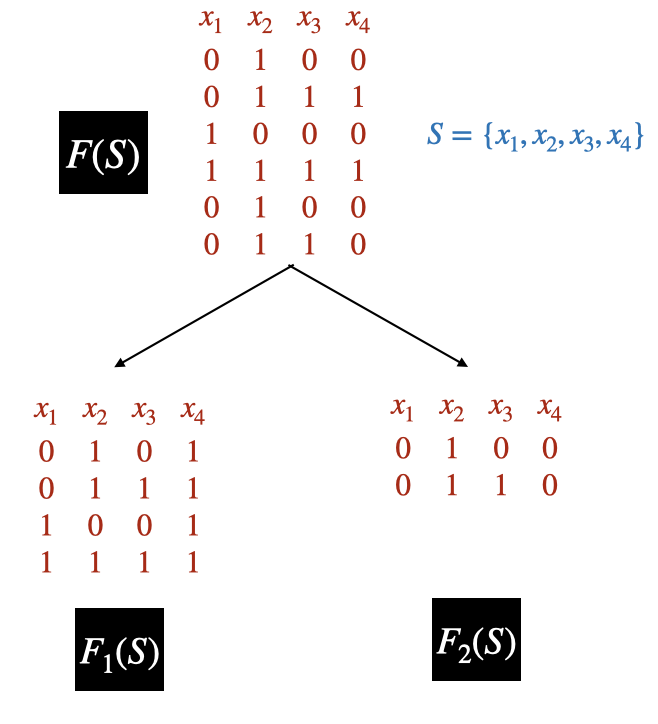
Consider the case of $F_1$. It's obvious that $VC(F_1) \leq VC(F) \leq d$. Now, $|F_1(S)|=|F_1(S \setminus \{x_m\})|$, since every labeling in $F_1(S)$ which is of the form $\{f(x_1),f(x_2),f(x_3), \cdots, f(x_{m-1}),1 \}$, $$\{f(x_1),f(x_2),f(x_3), \cdots, f(x_{m-1}) \} \in F_1(S\setminus \{x_m\})$$ So $|F_1(S)| \leq |F_1(S\setminus \{x_m\})|$.
Let $\{f^{'}(x_1),f^{'}(x_2),f^{'}(x_3), \cdots, f^{'}(x_{m-1}) \} \in F_1(S\setminus \{x_m\})$, then
$$\{f^{'}(x_1),f^{'}(x_2),f^{'}(x_3), \cdots, f^{'}(x_{m-1}),1 \} \in F_1(S)$$ So, $|F_1(S\setminus \{x_m\})| \leq |F_1(S)| $.
Then $$|F_1(S)| = |F_1(S\setminus \{x_m\})| \leq \Phi_{d}(m-1)=\sum\limits_{i=0}^{d} {m-1\choose i}$$For $F_2$ $$|F_2(S)|=|F_2(S\setminus\{x_m\})|$$
If $T$ is shattered by $F_2$, then $T\cup \{x_m\}$ must be shattered by $F$ since $\forall f_2 \in F_2, \exists \, f_1 \in F_1$ such that $f_1(x_i)=f_2(x_i)$, $\forall \, i=1,2,\cdots, m-1$ and $f_1(x_m)=1, f_2(x_m)=0$ (In Figure 1, $F_2$ shatters $\{x_3\}$ then $F$ shatters $\{x_3,x_4\}$).$ VC(F_2) \leq VC(F)-1 \leq d-1$.
$$ |F_2(S)| \leq \Phi_{d-1}(m-1)=\sum\limits_{i=0}^{d-1} {m-1\choose i}$$
So, $|\mathscr{H}(S)|=|F(S)|=|F_1(S)|+|F_2(S)| \leq \sum\limits_{i=0}^{d} {m-1\choose i} + \sum\limits_{i=0}^{d-1} {m-1\choose i}$
$\implies |\mathscr{H}(S)| \leq \sum\limits_{i=0}^{d} {m-1\choose i} + \sum\limits_{i=0}^{d-1} {m-1\choose i}$
$\implies |\mathscr{H}(S)| \leq {m\choose 0} + \sum\limits_{i=1}^{d} {m-1\choose i} + \sum\limits_{i=1}^{d} {m-1\choose i-1}$ (Since ${m\choose 0}={m-1\choose 0}$)
$\implies |\mathscr{H}(S)| \leq {m\choose 0} + \sum\limits_{i=1}^{d} {m\choose i}$ (Since ${m-1\choose k}+{m-1\choose k-1}={m\choose k}$, which comes from $(1+X)^m=(1+X)^{m-1}(1+X)$. See here for more information.)
$\implies |\mathscr{H}(S)| \leq \Phi_{d}(m)= \sum\limits_{i=0}^{d} {m\choose i}$So it proves the theorem.
Corollary
$\textbf{Corollary 3.1:}$ $\Phi_{d}(m)<2^m$ if $d < m$.
$\textbf{Proof:}$ We know, $\Phi_{d}(m)=\sum\limits_{i=0}^{d} {m\choose i}$ and $$ (1+x)^m=\sum\limits_{i=0}^{m} {m\choose i}1^ix^{m-i}$$Take x=1, then
$$2^m=\sum\limits_{i=0}^{m}{m\choose i}$$
So $\Phi_{d}(m)=\sum\limits_{i=0}^{d} {m\choose i}< \sum\limits_{i=0}^{m} {m\choose i}=2^m$ (if $d < m$).