Part 1: VC Dimension - Definition and Examples

This is the first part of the VC Dimension and Neural Networks series. Basic definition and some examples of vc dimension of learning algorithms are explained here.

1. Definition

Let $S=\{x_1,x_2,\cdots,x_m\}$ be the set of m random points from $\mathbb{R}^d$ and $\mathscr{H}$ be a class of $\{-1,+1\}$ valued functions on $\mathbb{R}^d$ i.e $$\forall \\, h \in H, h:S \to \{0,1\}^m$$ One such example is $h_1(x_i)=1 \,\forall \, x_i \in S$. In the context of Machine Learning, $\mathscr{H}$ is the learning algorithm generally used for any classification task such as Logistic Regression etc. For each parameter $\theta$ in Logistic Regression we get $h(\theta;x) \in \mathscr{H}$.

$\textbf{Shattering:}$ $S$ is shattered by $\mathscr{H}$ when all labeling of $S$ (with 0 and 1) can be computed by $\mathscr{H}$ i.e for all labeling of $S$ denoted by $Y=\{0,1\}^m$, $\exists \\, h\in \mathscr{H}$ such that the $\sum_{i}|h(x_i)-y_i|=0$, where $y_i$ is the label of the ith point. Consider in Figure 1, $S$ is the set of three points, $\mathscr{H}=\{wx+b;w,b\in \mathbb{R}\}$, for every possible labels of $S$ (colors of $S$), there is a line which achieves the classification task. So $\mathscr{H}=\{wx+b;w,b\in \mathbb{R}\}$ shatters $S$ (from Figure 1).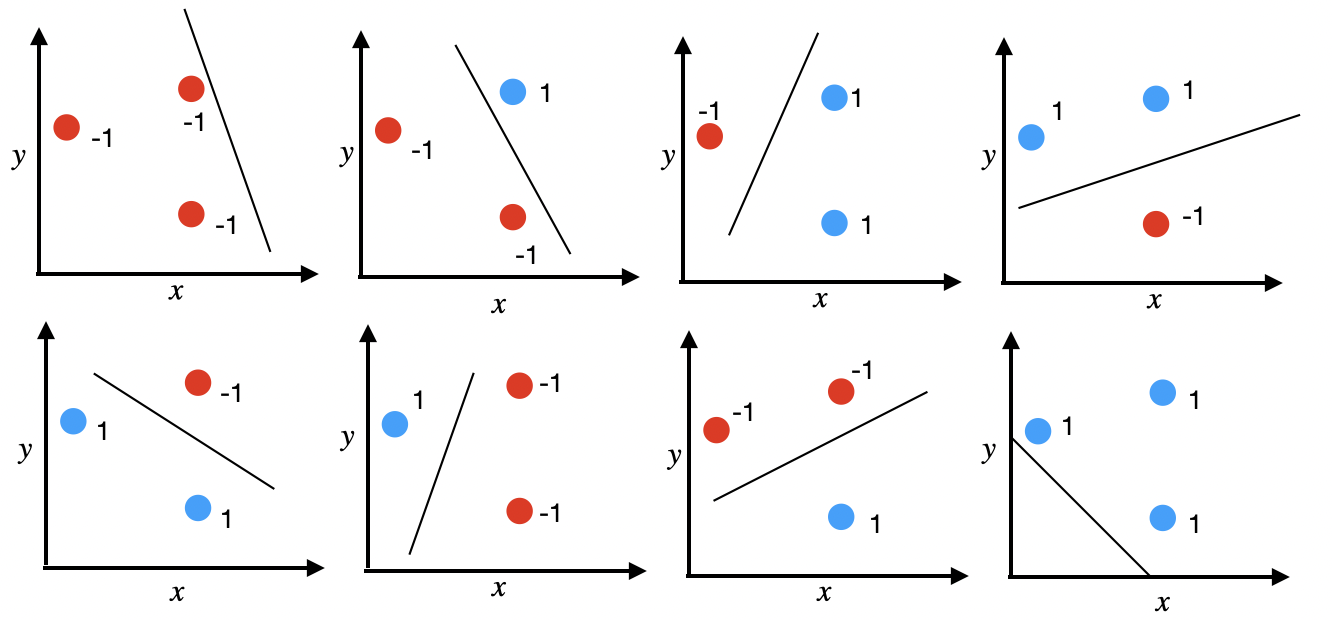

$\textbf{Vapnik-Chervonenkis (VC) dimension}$ of a hypothesis space($\mathscr{H}$) is the cardinality of the largest $S$ such that $\mathscr{H}$ shatters $S$. If $VC(\mathscr{H})=n$, there there exists $n$ points which can be shattered by $\mathscr{H}$ but no set of $(n+1)$ points can be shattered.

2. VC-dimension of class of Thresholds in $\mathbb{R}$

Let $\mathscr{H}$ be the class of thresholds i.e $\forall h_a \in \mathscr{H}$, $$h_a(x)=\begin{cases} 1 \, \text{if } x\geq a \\ -1 \, \text{if } x< a \\ \end{cases}$$

When $|S|=1$, it can be shattered by $\mathscr{H}$. For $|S|=2$ it's impossible to shatter since we can't find a threshold for third example (Figure 2). So $VC(\mathscr{H})=1$

3. VC-dimension of class of Intervals in $\mathbb{R}$

Let $\mathscr{H}$ be the class of intervals i.e $\forall h([a,b];x) \in \mathscr{H}$, $$h_a(x)=\begin{cases} 1 \, \text{if } x\in [a,b] \\ -1 \, \text{if } x \notin [a,b] \\ \end{cases}$$

Sample of 2 points can be shattered by $\mathscr{H}$ by taking the positive label in an interval.

But sample of 3 points can’t be shattered by $\mathscr{H}$, since there is no hypothesis that can predict the example where the middle value is negative (Figure 3). So $VC(\mathscr{H})=2$.

$\textbf{General Case:}$ For hypothesis class of k non-intersecting intervals ($\mathscr{H}^{k}$), VC dimension is $2k$ since every 2 points can be satisfied using one interval. But no sample with $2k+1$ points can be shattered since points with alternating positive and negative points can't be shattered by k intervals. (Figure 4)

$\textbf{Proof:}$ Let $S=\{x_1,x_2,\cdots,x_{2k+1} \}$. Label S such that $x_{2i+1}=1, x_{2i}=-1, \forall i=0,1,\cdots,k$.
Then there are $k+1$ positive examples. Since every positive example sits between two negative examples, every interval contains only one positive example. But there are only k intervals. So all the positive examples can't be covered. So $VC(\mathscr{H}^{k})=2k+1$.

4. VC-dimension of class of axis-aligned rectangles in $\mathbb{R}^2$

Let $\mathscr{H}$ be the set of rectangles whose sides are parallel to the axes. Then it can shatter a set of 4 points. So $VC(\mathscr{H})\geq 4$ (Figure 5).

5. VC-dimension of class of Line in $\mathbb{R}^2$

$\textbf{Theorem}:$ VC dimension of $\mathscr{H}=\{h;h(x)=sign(wx+b); w,b\in \mathbb{R}\}$ in $\mathbb{R}^2$ is 3 (Figure 1).

$\textbf{Proof}:$ Figure 1 shows a configuration of 3 points that can be shattered by $\mathscr{H}$. So, $VC(\mathscr{H}) \geq 3$. Now we have to prove that no set of 4 points can be shattered by $\mathscr{H}$.
Consider the set $S_4=\{x_1,x_2,x_3,x_4\}$. Now if we create a convex hull of S and label the diagonal points as same class, then no line can't classify S. So $VC(\mathscr{H})= 4$.

6. VC-dimension of class of hyperplane in $\mathbb{R}^d$

$\textbf{Theorem}:$ VC dimension of $\mathscr{H}=\{h;h(X)=sign(W^TX+b); W \in \mathbb{R}^d ,b\in \mathbb{R}\}$ in $\mathbb{R}^2$ is d.[1]

$\textbf{Proof}:$ We will first prove the lower bound.
Let $S=\{x_1,x_2,x_3,\cdots,x_d\} \cup \{x_{d+1}=0\}$ and $\{x_1,x_2,x_3,\cdots,x_d\}$ is the standard basis of $\mathbb{R}^d$ $$\begin{align} x_1 = \begin{bmatrix} 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix}\quad x_2 = \begin{bmatrix} 0 \\ 1 \\ \vdots \\ 0 \end{bmatrix}\cdots x_d = \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 1 \end{bmatrix} \end{align}$$ Let $Y=\{y_1,y_2,\cdots,y_d \}$ is a class label for S with $y_i\in \{-1,+1\}\, \forall \, i$, then $$h(X)=sign(\sum_i [x_i;1]\hat{W}),\hat{W}=[W;b]$$ can classify S. $$\begin{align} [x_i;1] = \begin{bmatrix} 0\\ 0 \\ \vdots \\ i\\ \vdots\\ 0\\ 1 \end{bmatrix} \end{align}$$
This is because the augmented set $\{[x_1;1],[x_2;1],\cdots, [x_d+1,1]\}$ is linearly independent and since its cardinality is $d+1$, it's a basis of $\mathbb{R}^{d+1}$. To prove that it's linearly independent, consider $\sum_i^{d+1} [x_i;1]\alpha_i =0$. $$ \begin{bmatrix} 1 & 0 &\cdots 1\\ 0 & 1 &\cdots 1\\ \vdots \\ 0& 0 &\cdots 1 \end{bmatrix} \begin{bmatrix} \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_{d+1} \end{bmatrix}= \begin{bmatrix} 0 \\ 0 \\ \vdots \\ 0 \end{bmatrix} $$ Then $\alpha_1=0,\alpha_2=0,\cdots, \alpha_{d+1}=0$. So the augmented set is linearly independent and a basis of $\mathbb{R}^{d+1}$. So $$h(X):sign(\sum_i [x_i;1]\hat{W})=Y$$ will always have a closed form solution. (One trick is to solve $[X;1]\hat{W}=Y \implies \hat{W}=[X;1]^{-1}Y, [X;1]=[[x_1;1] \,[x_2;1]\cdots \,[x_{d+1};1] $).
Then there exists a set of $d+1$ points that $\mathscr{H}$ can shatter. So $VC(\mathscr{H})\geq d+1$

Now we will try to prove the upper bound ($VC(\mathscr{H})\leq d+1$).
Let $S^{'}=\{x_1,x_2,\cdots, x_{d+2}\}$ be the set of $d+2$ points that $\mathscr{H}$ can shatter. Then we will get $W_i$ for every $2^{d+1}$ possible labeling such that $h(X)=sign([X;1]W_i)$. Let $W=[W_1^T \, W_2^T \, W_3^T \cdots \, W_{2^{d+2}}^T]$ be the vector containing all the $2^{d+2}$ weights. $$\begin{align} h(X) = \begin{bmatrix} [x_1;1] \\ [x_2;1] \\ \vdots \\ [x_{d+2};1] \end{bmatrix} \begin{bmatrix} W_1^T W_2^T W_3^T W_4^T \cdots W_{2^{d+2}}^T\\ \end{bmatrix}\\ h(X)= \begin{bmatrix} W_1^T[x_1;1] & W_2^T[x_1;1] & \cdots \cdots & W_{2^{d+2}}^T[x_1;1] \\ W_1^T[x_2;1] & W_1^T[x_2;1] & \cdots \cdots & W_{2^{d+2}}^T[x_2;1] \\ \vdots & \vdots & \ddots & \vdots\\ \vdots & \vdots & \quad \quad \quad \quad \quad\ddots & \vdots\\ W_1^T[x_{d+2};1] & W_1^T[x_{d+2};1] & \cdots \cdots & W_{2^{d+2}}^T[x_{d+2};1] \end{bmatrix} \end{align}$$

The upper bound can also be proven using Radon's Theorem which states that any set $S \subset R^{d}$ with $|S|=d+2$ can be partitioned into two disjoint subsets $S_1$ and $S_2$ whose convex hulls intersect which means it can't be separated by a hyperplane for all possible labeling, hence it can't be shattered by $\mathscr{H}$.

So $VC(\mathscr{H})=d+1$.

7. Bibliography

1. https://mlweb.loria.fr/book/en/VCdimhyperplane.html